In the past few years, very high precision, numerically controlled machine tools have been developed. To achieve the potential precision of these tools, length and displacement measurements whose resolution exceeds the least significant digit of the tool must be made. The measurement equipment typically would not rely on mechanical scales.
Laser interferometers compare the changes in optical path length to the wavelength of light, which can be chosen from atomic constants that can be determined with very little uncertainty. In 1983, there was a redefinition of the meter [1] that was previously defined in 1960. The old definition was based on the wavelength of a certain radiation (the krypton-86 standard) that could not be realized to better than 4 parts in 109 . The new definition, being based on frequency but not related to any particular radiation, opened the way to significant improvements in the precision with which the meter can be realized. As recommended in resolution 2 for the practical realization of the meter, the wavelength in vacuum λv of a plane electromagnetic wave of frequency f is λv = c/f, where c is the speed of light in vacuum, c = 299, 792, 458 m s–1 exactly. This way, the wavelength is related to frequency and time, which can be measured with the highest precision of all units within the Système International (SI).
In order to be independent of any environmental parameters, the meter is defined using the speed of light in a vacuum. However, interferometers usually must operate in ambient air. Thus, environmental parameters that influence the speed of light in a particular medium (air) will affect and degrade the precision of the measurement.
Three major factors limit the absolute accuracy attainable with laser interferometers operating in ambient air: (1) the uncertainties of the vacuum wavelength, λv, of the laser source; (2) the uncertainty of the refractive index of the ambient air; and (3) the least count resolution of the interferometer.
This chapter section is organized as follows. First, some basic laser principles are detailed, including ways to stabilize the vacuum wavelength of the laser. The effect most often used to stabilize lasers in commercial interferometers is the Zeeman effect, which yields relative uncertainties of 10–8.
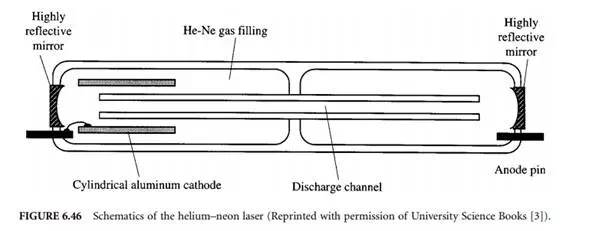
Second, the refractive index of air as another major factor limiting the attainable accuracy of laser interferometers operated in air is addressed. It is shown that it cannot be determined currently with uncertainty better than 5 × 10^–8.
And finally, the chapter section describes the most widely used Michelson interferometer and two of its variants for long-travel length measurement and gives their resolution.
Helium–Neon Laser
In order to attain the best possible accuracy, great care must be taken to ensure the highest wavelength stability of the light source. Almost all interferometric dimensional gages utilize a helium–neon laser because it has proven reliable, its emitted wavelength is in the visible range at about 633 nm, and it can be stabilized sufficiently well utilizing the Zeeman effect and to an even higher degree with the use of a very well-defined iodine absorption line also at ≈633 nm [1, 2].
The helium–neon laser consists of a discharge tube as shown in Figure 6.46 [3] filled with the single isotope gases helium (He3 ) at a partial pressure of ≈105 Pa and neon (Ne20) with a partial pressure of ≈13 Pa. It is pumped electrically using a voltage on the order of kilovolts with a current of a few milliamperes to excite both helium and neon atoms. Since the helium gas is the majority component, it dominates the discharge properties of the laser tube. Neutral helium atoms collide with free electrons that are accelerated by the axial voltage and become excited and remain in two rather long-lived metastable states. These are close enough to the energy levels of certain excited states of neon atoms so that collisional energy transfer can take place between these two groups of atoms. Excited helium atoms may drop down to the ground state, while simultaneously neon atoms take up almost exactly the same amount of energy. Therefore helium only serves to excite neon atoms, they do not contribute to the emission of light. The excited neon atoms remain in the excited state for a rather long period of time (on the order of 10–3 s). They return to lower energetic levels by stimulated emission of highly coherent light. This stimulated emission comes into effect when light emitted by some neon atoms also prompts other atoms to emit. The mirrors of the laser cavity, by reflecting most of the incident light cause the light to traverse multiple paths through the active laser volume, thereby greatly amplifying the light if the cavity length L is an integer multiple m of half the wavelength λ.
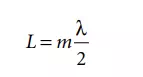
The emitted light is fairly monochromatic, but still has some finite spectral linewidth determined by the random emissions of Ne20.
Brewster angle [4] end windows of the discharge tube transmit light of the proper linear polarization if desired. The end mirrors have to be carefully polished. Their curvature radii have to satisfy the condition for stability. They have wavelength–selective dielectric coatings of very high reflectivity sometimes exceeding 99%.
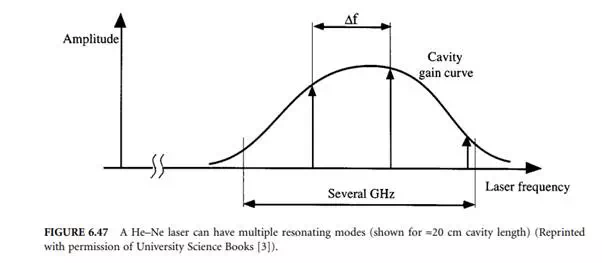
Unless special precautions are taken, a He–Ne laser will emit several axial modes as shown schematically in Figure 6.47, resulting in a beat frequency that limits the temporal coherence and renders the laser unsuitable for interferometric purposes. Also, due to thermal expansion of the laser tube, the end mirrors will change their relative distance, thereby effectively tuning the wavelength within the linewidth of the gain curve.
Another important property of a high-quality He–Ne laser is its Gaussian cross-sectional profile, which is maintained along a propagating wave, i.e., fundamental lateral mode. It is also a necessary condition for the wave fronts to remain quasiplanar.