The resonant frequency (and the wavelength λ) of the laser is determined in part by the distance between the two end mirrors and also by the refractive index nM of the active medium (the He–Ne mixture). Since the linewidth of the gain profile of the active medium is usually in the gigahertz range, multiple axial modes can resonate in the cavity as is shown in Figure 6.47. The frequency difference ∆f between two adjacent longitudinal modes is the free spectral range (FSR), which is given by Equation 6.71 and depends only on the cavity length, L, the refractive index of the active medium, nM, and the speed of light in vacuum, c.
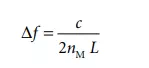
Due to thermal expansion of the laser cavity and/or thermally induced change in refractive index of the active medium, all resonating laser modes will move within the envelope of the gain profile. The effort undertaken in stabilizing the laser wavelength or equivalently stabilizing its frequency is aimed at locking the modes with respect to the gain profile and reducing the number of modes resonating simultaneously.
Longitudinal Zeeman Effect
One of the most often used effects in stabilizing the frequency of a He–Ne laser for distance measurements is the Zeeman effect [3, 5].
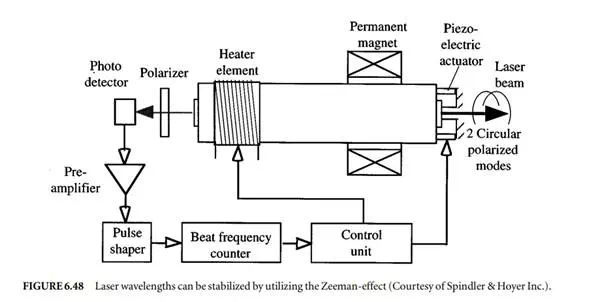
The tube of the laser whose frequency is to be stabilized is mounted inside an axial permanent magnet as shown in Figure 6.48. Because of a short cavity length chosen, the free spectral range ∆f of the laser is large. Therefore, the laser emission appears as a single longitudinal mode when the cavity length is properly controlled. An externally applied magnetic field in longitudinal direction causes the transition frequencies of the neon atoms to split symmetrically to the nominal frequency, the separation in frequency being proportional to the magnetic field strength. This phenomenon is called the longitudinal Zeeman effect.
With the applied field strength, the single longitudinal laser mode of the He–Ne laser is split into right and left circularly polarized modes with a frequency difference of typically 1.5 MHz. The frequency difference depends on the laser frequency and exhibits an extreme value when the laser frequency matches exactly the atomic transition frequency. Frequency stabilization is accomplished with control of the cavity length so that the frequency is locked to the extreme value corresponding to the nominal frequency of the laser. In order to determine the actual laser frequency within the gain profile, the cavity length is periodically modulated with a piezoelectric actuator shown in Figure 6.48. The frequency difference is constantly monitored at the minimum and maximum elongation of the modulation cycle. In the case when the extremal values are identical, the difference frequency will assume a maximum and thus the nominal value of the laser frequency is attained. This is achieved by controlling the length of the laser cavity. The cavity length is controlled both by using the thermal expansion of the laser tube, which is in close proximity to an electric heater whose operating current can be varied on a less dynamic scale, and on a very short time basis with a piezoelectric actuator attached to one of the end faces of the cavity [5]. This fast actuator allows for only a limited amplitude, typically on the order of less than a wavelength. Therefore, the thermal expansion must be used to attain greater modulation amplitude. To obtain the highest possible stability of the laser frequency, the frequency differences are measured within a very short time interval, and the determined deviations from the nominal value are fed back in a closed control loop to the electromechanical and thermal positioning devices.
The short- and long-term frequency stability ∆f/f of such a stabilized laser can be as high as 2 × 10–8, depending also on the parameters of the feedback loop.
Another phenomenon that exceeds the stabilization attainable with the Zeeman effect by far uses a particular absorption line of an iodine isotope (127I2, transition 11-5, R(127), component i) and locks the He–Ne laser [2, 6] in that very well-defined frequency. Its wavelength λI = 632.9913981 nm is very close to one of the nominal wavelengths of the He–Ne laser, so this can easily be accomplished; however, the necessary equipment including the sophisticated electronics is rather involved [2]. For this reason, iodine-stabilized He–Ne lasers are only used where very high precision is required.
The overall estimated relative uncertainty of such a stabilized laser is ±10–9 (which results from an estimated relative standard deviation of 3.4 × 10–10 [1]), which makes it suitable for the practical realization of the definition of primary and secondary standards.