Piezoelectricity, discovered in Rochelle salt in 1880 by Jacques and Pierre Curie, is the term used to describe the ability of certain materials to develop an electric charge that is proportional to a direct applied mechanical stress. These materials also show the converse effect; that is, they will deform (strain) proportionally to an applied electric field. Some crystalline materials show piezoelectric behavior due to their unique crystal structure. The lattice structure of a crystal is described by the Bravais unit cell [1]. There are 230 microscopic symmetry types (space groups) in nature, based on the several symmetry elements such as translation, inversion center, mirror plane, or rotation axes. Combinations of these symmetry elements yield the macroscopic symmetry known as point groups. All-natural crystals can be grouped into 32 different classes (point groups) based on their symmetry elements. The 32-point groups can be further classified into two subgroups: (1) crystals with a center of symmetry, and (2) crystals with no center of symmetry. The 11 centrosymmetric subgroups do not show piezoelectricity. Of the 21 non-centrosymmetric groups, 20 show the piezoelectric effect along unique directional axes. An important class of piezoelectric materials includes ferroelectrics, in which the piezoelectric effect is closely related to the ferroelectric polarization that can be reversed by the application of sufficiently high electric field [2, 3]. To induce piezoelectric properties in ferroelectric materials, a poling procedure is often required, which consists of the temporary application of a strong electric field. Poling is analogous to the magnetizing of a permanent magnet.
Governing Equations and Coefficients
The phenomenological master equation describing the deformations of an insulating crystal subject to both elastic and electric stress is given by



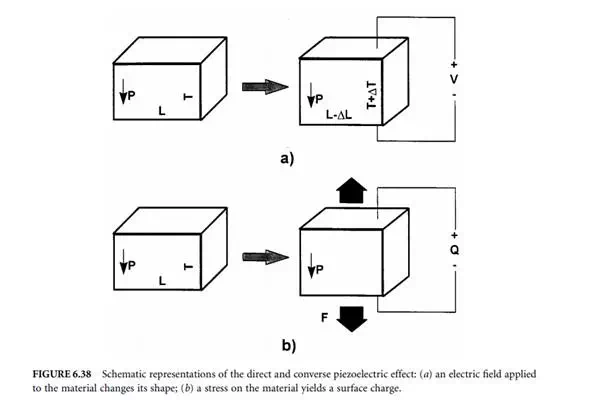
where Pm is the component of electrical polarization. The difference between the direct and converse piezoelectric effect is shown schematically in Figure 6.38. The converse effect describes the actuating function of a piezoelectric, where a controlled electric field accurately changes the shape of a piezoelectric material. The sensing function of a piezoelectric is described by the direct effect, where a controlled stress on a piezoelectric material yields a charge proportional to the stress.


where εii is the dielectric constant (relative permittivity), and ε0 is the permittivity of free space (8.854 × 10–12 F m–1). Another key property of piezoelectric materials is their electromechanical coupling coefficient k, defined as:

The value of k represents the efficiency of the piezoelectric in converting one form of energy to another. Since energy conversion is never complete, the value of k2 is always less than unity, so k is always less than 1.
Two final important parameters for piezoelectric (ferroelectric) materials are their Curie point (T0 ) and Curie temperature (Tc). The Curie point is the temperature above which the material loses its ferroelectric and piezoelectric behavior. The Curie temperature is defined by the Curie-Weiss law.
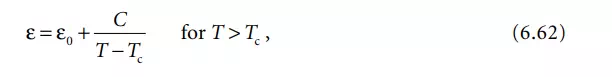
where ε is the dielectric constant of the material, C is the Curie–Weiss constant, and T is the temperature. It represents the temperature where the material tends to have its highest dielectric constant. The Curie temperature is always lower (often within 10°C) than the Curie point.