Electrical engineers come across very large and very small numbers compared to everyday experience. This article gives you an initial exposure to large and small numbers and has examples of how they show up in engineering applications. Engineering numbers are written in engineering notation, similar to scientific notation. It helps to get comfortable with engineering notation and the wide, dynamic range of numbers that engineers deal with on a regular basis.

Scientific notation

If you’ve studied math or science, you have probably run across scientific notation. You can brush up on scientific notation with this video. To express a number in scientific notation, you rewrite it as a number \ge1≥1is greater than or equal to, 1 and \lt10<10, multiplied by a power of 101010. It might make more sense if we look at some examples:

Engineering notation

The habit in engineering is to use a slightly modified scientific notation. Engineers like exponents in multiples of three. This means the digits to the left of the decimal point fall in the range of one to 999. Our minds do a pretty good job relating to numbers in this range. Engineering notation is only slightly different than scientific notation.

It takes light 0.0000333564095 seconds to travel 10 kilometers in a vacuum. Let’s convert this small number into engineering notation:

·         Find the decimal point.

·         Hop over three digits at a time, going right, until you hop over one, two, or three nonzero digits. In this case, take two hops to the right, until you hop over 333333.

·         Write down 333333.

·         Add a decimal point: 33.33.33, point

·         Write down the remaining digits: 33.356409533.356409533, point, 3564095.

·         Because we hopped right, finish by writing 101010 raised to the negativenumber of hops times three: -2 \,\text{hops} \times 3 = -6−2hops×3=−6minus, 2, space, h, o, p, s, times, 3, equals, minus, 6. 33.3564095 \times10^{-6}33.3564095×10−633, point, 3564095, times, 10, start superscript, minus, 6, end superscript seconds is the time it takes for light to travel 10 kilometers in a vacuum, in engineering notation.

A few more examples of engineering notation:

·         Speed of light: 300 \times 10^6\,\text{m/s}300×106m/s300, times, 10, start superscript, 6, end superscript, space, m, slash, s

·         A blink of an eye: {\sim} 350 \times 10^{-3}\,\text s∼350×10−3sThe number format rules are not rigid. As long as the point you are trying to make is clear and unambiguous, you may make exceptions. The blink of an eye may be clearly written 0.350 seconds if you intend the reader to compare the value to one second.

One flaw in engineering notation is that it can mislead about the number of significant figures. Engineers generally deal with wide tolerances of manufactured components, so the number of significant figures in circuit designs is usually small: two to three. If the tolerance is important, it is common to write it next to the number, as shown in this example:

A large resistance value: 33.3 \times 10^6 \,\Omega\:\:\pm1\%33.3×106Ω±1%. Over time, you will develop a feel for numerical accuracy and rounding in different situations. When done appropriately, rounding to a few digits is not a sign of laziness, but a realization that real-world components are not all the same—and yet your design still has to work every time. There are other instances, such as during long calculations using computer arithmetic, where even tiny rounding errors are important to anticipate and control. It all depends on the situation. This is the engineering art.

Prefixes

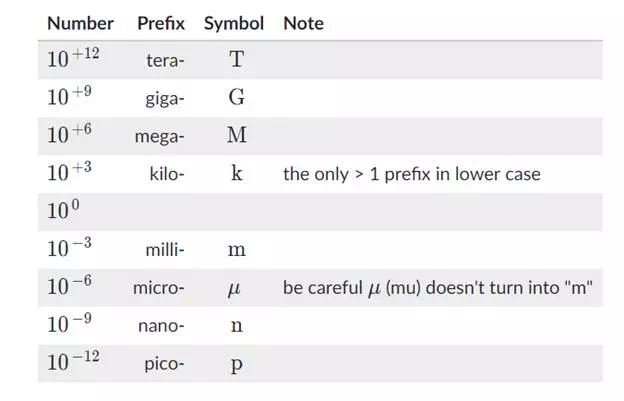
Many numbers have names derived from Greek or Latin. Engineers and scientists use Système International d’Unités (SI) number prefixes. Some of the most common prefixes in engineering are listed below. Notice that the exponents are multiples of three. These prefixes are shorter and easier to say or abbreviate than the numerical equivalent: “\times10 \text{ to the …}×10 to the …times, 10, space, t, o, space, t, h, e, space, point, point, point”.

numbers this large and small?

Yes! Below are examples of large, medium and small numbers used in real-world electrical systems. These examples are common occurrences, and you can always find greater extremes.

Frequency: Frequency counts the number of times something happens per second—or another unit of time. The SI unit for frequency is hertz (Hz), which is the same as 1/s1/s1, slash, s. You could also say “reciprocal second” or “per second”. The internal clock of a modern personal computer runs at a frequency of around 3 GHz (3 \times 10 ^{9}\,\text{Hz})(3×109Hz)left parenthesis, 3, times, 10, start superscript, 9, end superscript, space, H, z, right parenthesis. This corresponds to a clock period—the amount of time between clock ticks—of 1/(3 \times 10^9)1/(3×109)1, slash, left parenthesis, 3, times, 10, start superscript, 9, end superscript, right parenthesis or 333 ps (333 \times 10^{-12} \,\text{s})(333×10−12s)left parenthesis, 333, times, 10, start superscript, minus, 12, end superscript, space, s, right parenthesis. A human heart beats about one time per second (1 Hz), as detected by an electrocardiogram (ECG) machine.

Resistance: Resistance is measured in units of ohms (\Omega)(Ω). The resistance of a wire is often much less than one ohm. Resistance up to tens of megohms (10\times10^{6}\, \Omega)(10×106Ω) is not unusual.

Voltage: The unit of electrical potential is the volt (V). A flashlight battery is 1.5 volts. You can hold this battery in your hand without fear of electric shock. Inside a computer, the chips usually operate with 3 to 5 volts. A car battery is 12 volts. A wall socket is 110 or 220 volts, depending on where you live. This voltage can be fatal if you touch it with bare hands. High-tension power lines overhead are hundreds of thousands of volts—tension is the French word for voltage. As for tiny voltages, wireless signals are measured in microvolts (10^{-6}\,\text{V})(10−6V)left parenthesis, 10, start superscript, minus, 6, end superscript, space, V, right parenthesis when detected by a radio or mobile phone receiver.

Current: Currents are measured in amperes (A). One ampere is a large current. Car batteries momentarily supply 100 amperes or more to start a car. A house may consume 150 amperes if everything is turned on. Currents can also be absurdly small. There are situations where 1 femtoamp (1 \times 10^{-15} \,\text{A})(1×10−15A)left parenthesis, 1, times, 10, start superscript, minus, 15, end superscript, space, A, right parenthesis matters.

Time: Electrical circuits are capable of working at very short time scales. Time intervals in electronics range from 1 second, for the heartbeat example above, down to 1 picosecond (1\times10^{-12}\,\text{s})(1×10−12s)left parenthesis, 1, times, 10, start superscript, minus, 12, end superscript, space, s, right parenthesis.

Capacitance: Capacitance has units of farads (F). A farad is defined as a coulomb per volt. Since a coulomb is such a large amount of charge, a farad is a large unit of capacitance. As a result, capacitance values you come across are tiny numbers. 100 microfarads is a large capacitance. If you twist two 1-inch (2- centimeter) pieces of ordinary insulated hookup wire together, those wires have a capacitance around one picofarad (1 \times 10^{-12} \,\text F)(1×10−12F)left parenthesis, 1, times, 10, start superscript, minus, 12, end superscript, space, F, right parenthesis. 

Distance and Length: Distance and length have units of meters. We deal with huge distances and tiny lengths on a regular basis. Nature gives us some staggering distances—light travels at 300 \times 10^{6}300×106300, times, 10, start superscript, 6, end superscript meters (300 million meters) in one second. Modern microelectronics blesses us with astoundingly small dimensions inside integrated circuits. Today’s most aggressive—and expensive—integrated-circuit processes have dimensions as small as 15 nanometers (15 \times 10^{-9}\,\text m)(15×10−9m)left parenthesis, 15, times, 10, start superscript, minus, 9, end superscript, space, m, right parenthesis. That’s 15 billionths of a meter!

Unit grammar

These are the grammatical guidelines for writing unit names and symbols.

·         Names of all units start with a lowercase letter, even if the unit is named after a person.

·         Symbols for units are uppercase if the unit is named after a person, otherwise lowercase.

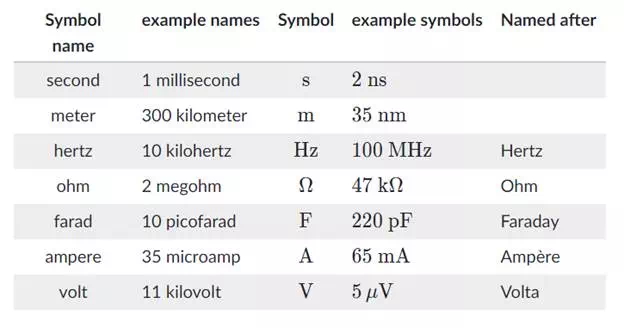
Isn’t it cool. Ohm gets a Greek symbol: \OmegaΩ, “Ohm ega.”