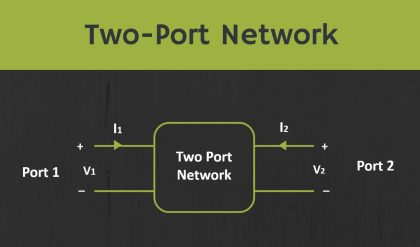
Procedure of two port parameter conversions

Follow these steps, while converting one set of two port network parameters into the other set of two port network parameters.

·        Step 1 − Write the equations of a two port network in terms of desired parameters.

·        Step 2 − Write the equations of a two port network in terms of given parameters.

·        Step 3 − Re-arrange the equations of Step2 in such a way that they should be similar to the equations of Step1.

·        Step 4 − By equating the similar equations of Step1 and Step3, we will get the desired parameters in terms of given parameters. We can represent these parameters in matrix form.

Z parameters to Y parameters

Here, we have to represent Y parameters in terms of Z parameters. So, in this case Y parameters are the desired parameters and Z parameters are the given parameters.

Step 1 − We know that the following set of two equations, which represents a two port network in terms of Y parameters.

I1=Y11V1+Y12V2I1=Y11V1+Y12V2

I2=Y21V1+Y22V2I2=Y21V1+Y22V2

We can represent the above two equations in matrix form as

[I1I2]=[Y11Y21Y12Y22][V1V2][I1I2]=[Y11Y12Y21Y22][V1V2]Equation 1

Step 2 − We know that the following set of two equations, which represents a two port network in terms of Z parameters.

V1=Z11I1+Z12I2V1=Z11I1+Z12I2

V2=Z21I1+Z22I2V2=Z21I1+Z22I2s

We can represent the above two equations in matrix form as

[V1V2]=[Z11Z21Z12Z22][I1I2][V1V2]=[Z11Z12Z21Z22][I1I2]

Step 3 − We can modify it as

[I1I2]=[Z11Z21Z12Z22]−1[V1V2][I1I2]=[Z11Z12Z21Z22]−1[V1V2]Equation 2

Step 4 − By equating Equation 1 and Equation 2, we will get

[Y11Y21Y12Y22]=[Z11Z21Z12Z22]−1[Y11Y12Y21Y22]=[Z11Z12Z21Z22]−1

⇒[Y11Y21Y12Y22]=[Z22−Z21−Z12Z11]ΔZ⇒[Y11Y12Y21Y22]=[Z22−Z12−Z21Z11]ΔZ

Where,

ΔZ=Z11Z22−Z12Z21ΔZ=Z11Z22−Z12Z21

So, just by doing the inverse of Z parameters matrix, we will get Y parameters matrix.