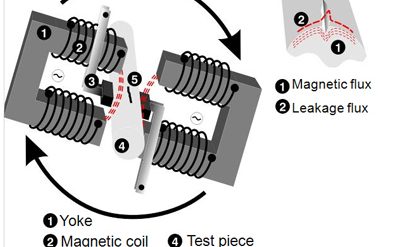
As mentioned earlier the transformer is a static device working on the principle of Faraday’s law of induction. Faraday’s law states that a voltage appears across the terminals of an electric coil when the flux linkages associated with the same changes. This emf is proportional to the rate of change of flux linkages. Putting mathematically

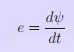
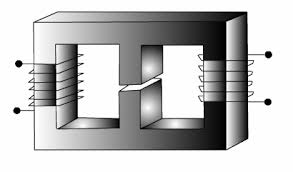
Where, e is the induced emf in volt and ψ is the flux linkages in Weber turn. Fig. 1 shows a

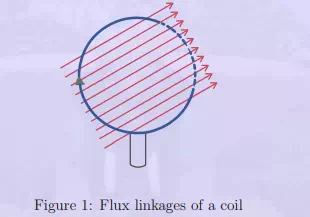
coil of N turns. All these N turns link flux lines of φ Weber resulting in the Nφ flux linkages. In such a case,

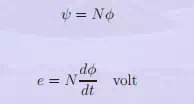
The change in the flux linkage can be brought about in a variety of ways

• coil may be static and unmoving but the flux linking the same may change with time.

• flux lines may be constant and not changing in time but the coil may move in space linking different value of flux with time.

• both 1 and 2 above may take place. The flux lines may change in time with coil moving in space.

These three cases are now elaborated in sequence below, with the help of a coil with a simple geometry

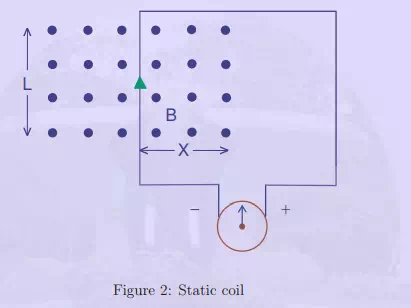
Fig. 2 shows a region of length L m, of uniform flux density B Tesla, the flux lines being normal to the plane of the paper. A loop of one turn links part of this flux. The flux φ linked by the turn is L ∗ B ∗ X Weber. Here X is the length of overlap in meters as shown in the figure. If now B does not change with time and the loop is unmoving then no emf is induced in the coil as the flux linkages do not change. Such a condition does not yield any useful machine. On the other hand if the value of B varies with time a voltage is induced in the coil linking the same coil even if the coil does not move. The magnitude of B

is assumed to be varying sinusoidally, and can be expressed as,

where Bm is the peak amplitude of the flux density. ω is the angular rate of change with time. Then, the instantaneous value of the flux linkage is given by,

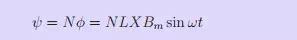
The instantaneous value of the induced emf is given by,

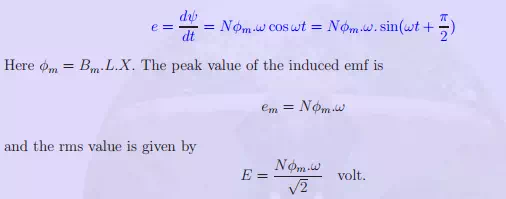
Further, this induced emf has a phase difference of π/2 radian with respect to the flux linked by the turn. This emf is termed as ‘transformer’ emf and this principle is used in a transformer. Polarity of the emf is obtained by the application of Lenz’s law. Lenz’s law states that the reaction to the change in the flux linkages would be such as to oppose the cause. The emf if permitted to drive a current would produce a counter mmf to oppose this changing flux linkage. In the present case, presented in Fig. 2 the flux linkages are assumed to be increasing. The polarity of the emf is as indicated. The loop also experiences a compressive force.

Fig. 2(b) shows the same example as above but with a small difference. The flux density is held constant at B Tesla. The flux linked by the coil at the current position is φ = B.L.X Weber. The conductor is moved with a velocity v = dx/dt normal to the flux, cutting the flux lines and changing the flux linkages. The induced emf as per the application of Faraday’s law of induction is e = N.B.L.dx/dt = B.L.v volt.(Here N=1)

Please note,the actual flux linked by the coil is immaterial. Only the change in the flux linkages is needed to be known for the calculation of the voltage. The induced emf is in step with the change in ψ and there is no phase shift. If the flux density B is distributed sinusoidally over the region in the horizontal direction, the emf induced also becomes sinusoidal. This type of induced emf is termed as speed emf or rotational emf, as it arises out of the motion of the conductor. The polarity of the induced emf is obtained by the application of the Lenz’s law as before. Here the changes in flux linkages is produced by motion of the conductor. The current in the conductor, when the coil ends are closed, makes the conductor experience a force urging the same to the left. This is how the polarity of the emf shown in fig.2b is arrived at. Also the mmf of the loop aids the field mmf to oppose change in flux linkages. This principle is used in d.c machines and alternators.

The third case under the application of the Faraday’s law arises when the flux changes and also the conductor moves. This is shown in Fig. 2(c).

The first term is due to the changing flux and hence is a transformer emf. The second term is due to moving conductor or is a speed emf. When the terminals are closed such as to permit a current the conductor experiences a force and also the mmf of the coil opposes the change in flux linkages. This principle is used in a.c. machines where the field is time varying and conductors are moving under the same. The first case where there is a time varying field and a stationary coil resulting in a transformer emf is the subject matter in the present section. The case two will be revisited under the study of the d.c machines and synchronous machines. Case three will be extensively used under the study of a.c machines such as induction machines and also in a.c. commutator machines.

Next in the study of the transformers comes the question of creating a time varying filed. This is easily achieved by passing a time varying current through a coil. The winding which establishes the field is called the primary. The other winding, which is kept in that field and has a voltage induced in it, is called a secondary. It should not be forgotten that the primary also sees the same time varying field set up by it linking its turns and has an induced emf in the same. These aspects will be examined in the later sections. At first the common constructional features of a transformer used in electric power supply system operating at 50 Hz are examined.