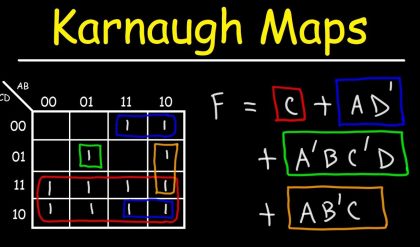
Hexadecimal describes a base-16 number system. That is, it describes a numbering system containing 16 sequential numbers as base units (including 0) before adding a new position for the next number. (Note that we’re using “16” here as a decimal number to explain a number that would be “10” in hexadecimal.) The hexadecimal numbers are 0-9 and then use the letters A-F.  Hexadecimal is a convenient way to express binary numbers in modern computers in which a byte is almost always defined as containing eight binary digits. When showing the contents of computer storage (for example, when getting a core dump of storage in order to debug a new computer program or when expressing a string of text characters or a string of binary values in coding a program or HTML page), one hexadecimal digit can represent the arrangement of four binary digits. Two hexadecimal digits can represent eight binary digits, or a byte.

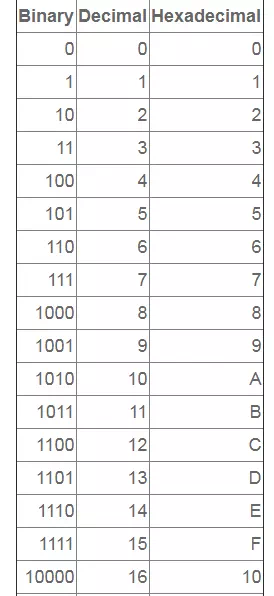
Hexadecimal Number SystemFollowing are the characteristics of a hexadecimal number system.·        Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.·        Letters represents numbers starting from 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.·        Also called base 16 number system.·        Each position in a hexadecimal number represents a 0 power of the base (16). Example − 160·        Last position in a hexadecimal number represents an x power of the base (16). Example − 16x where x represents the last position – 1.ExampleHexadecimal Number − 19FDE16Calculating Decimal Equivalent –Note − 19FDE16 is normally written as 19FDE. Hexadecimal AdditionFollowing hexadecimal addition table will help you greatly to handle Hexadecimal addition.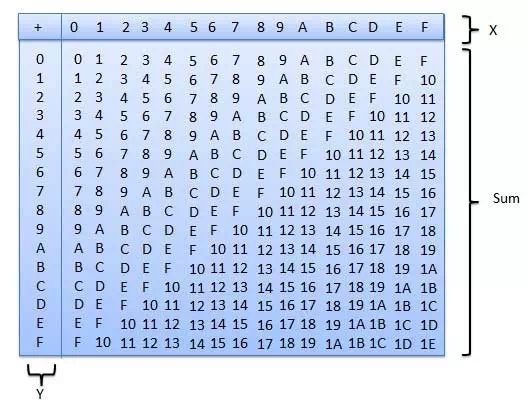To use this table, simply follow the directions used in this example − Add A16and 516. Locate A in the X column then locate the 5 in the Y column. The point in ‘sum’ area where these two columns intersect is the sum of two numbers.A16 + 516 = F16.Example − Addition    Hexadecimal SubtractionThe subtraction of hexadecimal numbers follow the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 1010. In the binary system, you borrow a group of 210. In the hexadecimal system you borrow a group of 1610.Example – Subtraction
Hexadecimal multiplication:Hex multiplication can be tricky because the conversions between hex and decimal when performing the operations require more effort since the numerals tend to be larger. Having a hexadecimal multiplication table can be helpful (one is provided below).Otherwise manual conversion between decimal and hex will be necessary for each step. Below is an example of hex multiplication. To the right of the example, each of the multiplication and addition steps are shown. Note that all of the numerals used are hex. Refer to the addition section if necessary.EX:  FA        3 × A = 1E; 1 carried to F×    C33 × F = 2D, + 1 = 2E 2EF        C × A = 78; 7 carried to F+  BB80C × F = B4, + 7 = BB=  BE6E
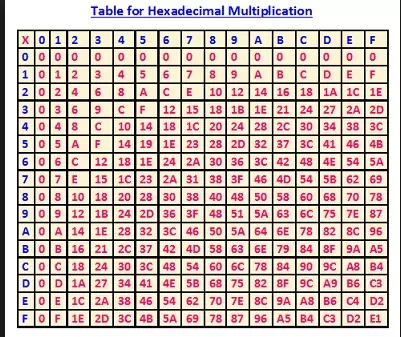Hex DivisionLong division in hex is identical to long division in decimal, except that the multiplication and subtraction occur in hex. It is also possible to convert to decimal and perform long division in decimal, then convert back once complete. For illustrative purposes, the division example will be calculated entirely in hex. As with multiplication, having a hexadecimal multiplication table (one is provided below) would be convenient while conducting hex division. Below is an example. Note that all numerals in the example are hex. Although no borrowing occurs in the example below, remember that borrowing in hex results in 16decimal being borrowed, rather than 10decimal. Refer to the hex subtraction section for further details.