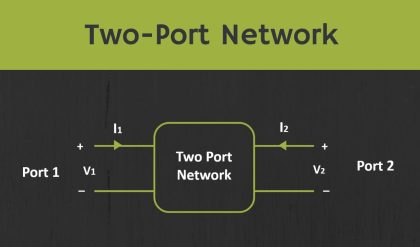
Procedure of two port parameter conversions
Follow these steps, while converting one set of two port network parameters into the other set of two port network parameters.
· Step 1 − Write the equations of a two port network in terms of desired parameters.
· Step 2 − Write the equations of a two port network in terms of given parameters.
· Step 3 − Re-arrange the equations of Step2 in such a way that they should be similar to the equations of Step1.
· Step 4 − By equating the similar equations of Step1 and Step3, we will get the desired parameters in terms of given parameters. We can represent these parameters in matrix form.
Z parameters to Y parameters
Here, we have to represent Y parameters in terms of Z parameters. So, in this case Y parameters are the desired parameters and Z parameters are the given parameters.
Step 1 − We know that the following set of two equations, which represents a two port network in terms of Y parameters.
I1=Y11V1+Y12V2I1=Y11V1+Y12V2
I2=Y21V1+Y22V2I2=Y21V1+Y22V2
We can represent the above two equations in matrix form as
[I1I2]=[Y11Y21Y12Y22][V1V2][I1I2]=[Y11Y12Y21Y22][V1V2]Equation 1
Step 2 − We know that the following set of two equations, which represents a two port network in terms of Z parameters.
V1=Z11I1+Z12I2V1=Z11I1+Z12I2
V2=Z21I1+Z22I2V2=Z21I1+Z22I2s
We can represent the above two equations in matrix form as
[V1V2]=[Z11Z21Z12Z22][I1I2][V1V2]=[Z11Z12Z21Z22][I1I2]
Step 3 − We can modify it as
[I1I2]=[Z11Z21Z12Z22]−1[V1V2][I1I2]=[Z11Z12Z21Z22]−1[V1V2]Equation 2
Step 4 − By equating Equation 1 and Equation 2, we will get
[Y11Y21Y12Y22]=[Z11Z21Z12Z22]−1[Y11Y12Y21Y22]=[Z11Z12Z21Z22]−1
⇒[Y11Y21Y12Y22]=[Z22−Z21−Z12Z11]ΔZ⇒[Y11Y12Y21Y22]=[Z22−Z12−Z21Z11]ΔZ
Where,
ΔZ=Z11Z22−Z12Z21ΔZ=Z11Z22−Z12Z21
So, just by doing the inverse of Z parameters matrix, we will get Y parameters matrix.