RLC Circuit:
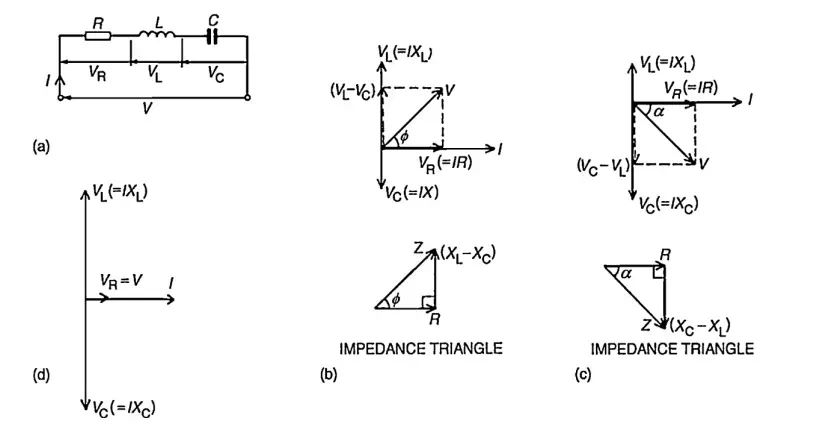
Consider a circuit in which R, L, and C are connected in series with each other across ac supply as shown in fig.
The ac supply is given by,
V = Vm sin wt
The circuit draws a current I. Due to that different voltage drops are,
1) Voltage drop across Resistance R is VR = IR
2) Voltage drop across Inductance L is VL = IXL
3) Voltage drop across Capacitance C is Vc = IXc The characteristics of three drops are,
1. VR is in phase with current I
2. VL leads I by 900
3. Vc lags I by 900
According to krichoff’s laws
Steps to draw phasor diagram:
1. Take current I as reference
2. VR is in phase with current I
3. VL leads current by 900
4. Vc lags current by 900
5. obtain resultant of VL and Vc. Both VL and Vc are in phase opposition (1800 out of phase)
6. Add that with VRby law of parallelogram to getsupply voltage.
The phasor diagram depends on the condition of magnitude of VL and Vc which ultimately depends on values of XL and Xc.
Let us consider different cases:
Case(i): XL > Xc
When X L > Xc
Also VL > Vc (or) IXL > IXc
So, resultant of VL and Vc will directed towards VL i.e. leading current I. Hence I lags V i.e. current I will lags the resultant of VL and Vc i.e. (VL – Vc). The circuit is said to be inductive in nature.
From voltage triangle,
V = √ (VR2 + (VL – Vc) 2) = √ ((IR) 2 + (IXL – IXc) 2)
V = I √ (R2 + (XL – Xc) 2)
V = IZ
Z = √ (R2 + (XL – Xc) 2 )
If , V = Vm Sin wt ; i = Im Sin (wt – ф)
i.e I lags V by angle ф
Case(ii): XL < Xc
When XL < Xc
Also VL < Vc (or) IXL < IXc
Hence the resultant of VL and Vc will directed towards Vc i.e current is said to be capacitive in nature Form voltage triangle
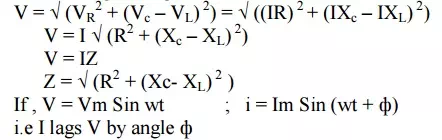
i.e I lags V by angle ф
Case(iii): XL = Xc
When XL = Xc
Also VL = Vc (or) IXL = IXc
So VL and Vc cancel each other and the resultant is zero. So V = VR in such a case, the circuit is purely resistive in nature.
Impedance:
In general for RLC series circuit impedance is given by,
Z = R + j X
X = XL – Xc = Total reactance of the circuit
If XL > Xc ; X is positive & circuit is Inductive
If XL < Xc ; X is negative & circuit is Capacitive
If XL = Xc ; X =0 & circuit is purely Resistive
Tan ф = [(XL – Xc )∕R]
Cos ф = [R∕Z]
Z = √ (R2 + (XL – Xc ) 2)
Impedance triangle:
In both cases R = Z Cos ф
X = Z Sin ф
Power and power triangle:
The average power consumed by circuit is,
Pavg = (Average power consumed by R) + (Average power consumed by L) + (Average power consumed by C)
Pavg = Power taken by R = I2R = I(IR) = VI
V = V Cos ф
P = VI Cos ф
Thus, for any condition, XL > Xc or XL < Xc General power can be expressed as
P = Voltage x Component in phase with voltage
Power triangle:
S = Apparent power = I2Z = VI
P = Real or True power = VI Cos ф = Active power
Q = Reactive power = VI Sin ф